Hello! I’m Seonho Kim!

I am a fifth-year Ph.D. student at the Ohio State University, working with Prof. Kiryung Lee. Prior to that, for my MS and BS degrees, I was fortunate to be advised by Prof. Songnam Hong at Ajou University in South Korea. My research interests span the algorithmic foundations in the fields of data science, machine learning, optimization, and signal processing.

Research Summary

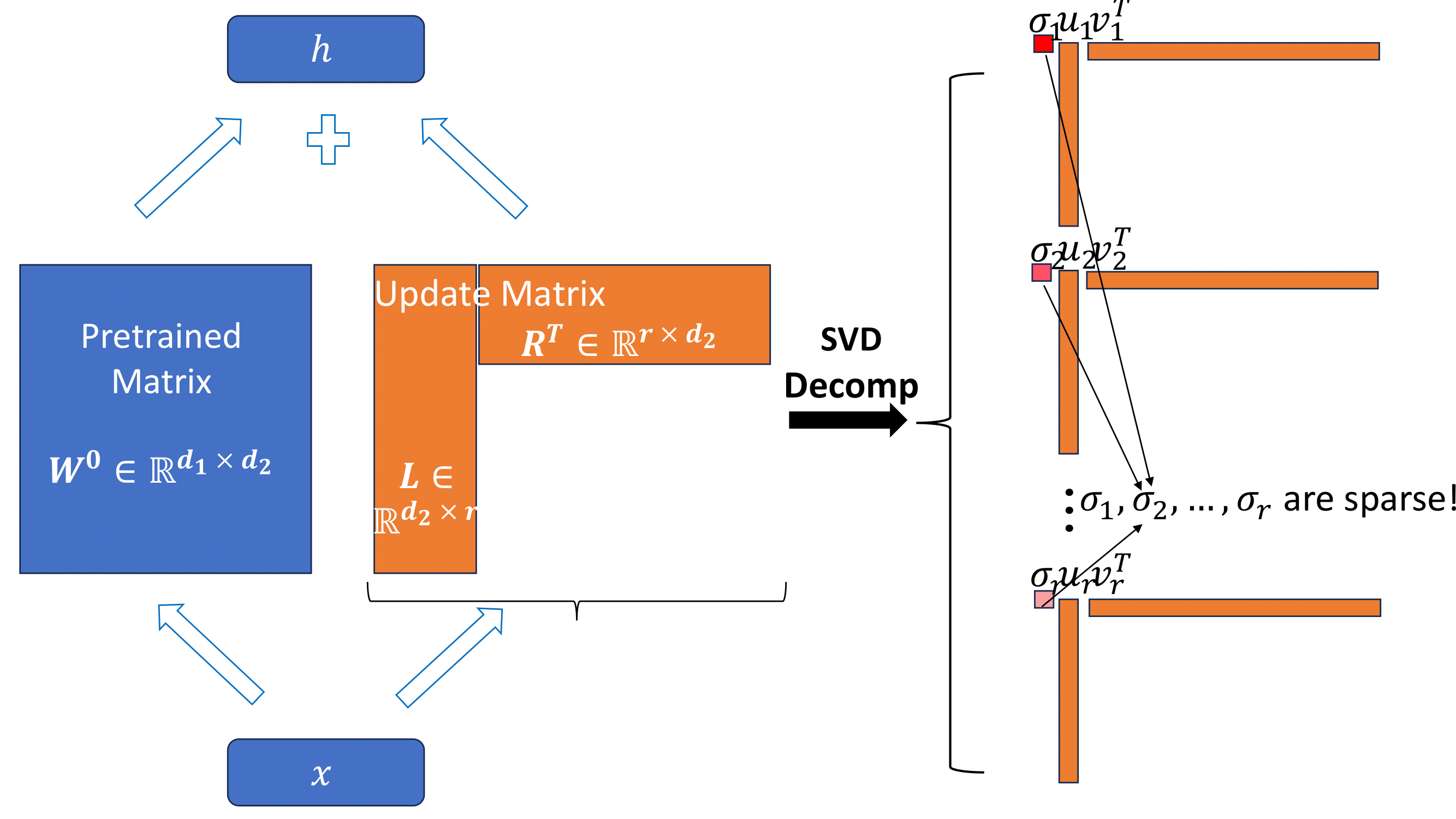
Parameter-Efficient Fine Tuning using Trace norm regularization

Low-Rank Adaptation (LoRA) is a representative, parameter-efficient fine-tuning method for large pre-trained models in downstream tasks. To enhance LoRA's parameter efficiency, we propose a novel pruning technique that utilizes the trace norm (also referred to as the nuclear norm) with matrix factorization. We demonstrate that our method outperforms baseline algorithms, including LoRA and AdaLoRA, on the GLUE benchmark dataset,achieving a 1.5% performance gain with 35% fewer parameters. This work is ongoing for publication.

TraceLoRA — An illustration of a low-rank matrix update using trace norm, where the updated matrix exhibits sparse singular values.

Robust Phase Retrieval via iterative Gauss-Newton Method

Phase Retrieval recovers a signal from the absolute value of its linear measurements, which arises in signal and imaging processing. We proposed an iterative Gauss-Newton method for phase retrieval in outlier scenarios and demonstrated that a linear program can solve a step of the Gauss-Newton method. Furthermore, we established that in outlier scenarios, the method converges to the ground-truth signal at a linear rate with near-optimal sample complexity with high probability. Lastly, we demonstrate that our proposed methods are computationally efficient and exhibit superior performance compared to the baseline algorithms. This work is to appear in ICASSP 2024

Project Image 1 Description — Image recovery of our algorithm: Left is true digit; middle is initialization; right is recovered image.

Project Image 2 Description — Image recovery of our algorithm: Left is true digit; middle is initialization; right is recovered image.

Project Image 4 Description — Image recovery of baseline algorithm: Left is true digit; middle is initialization; right is recovered image.

Project Image 5 Description — Image recovery of baseline algorithm: Left is true digit; middle is initialization; right is recovered image.

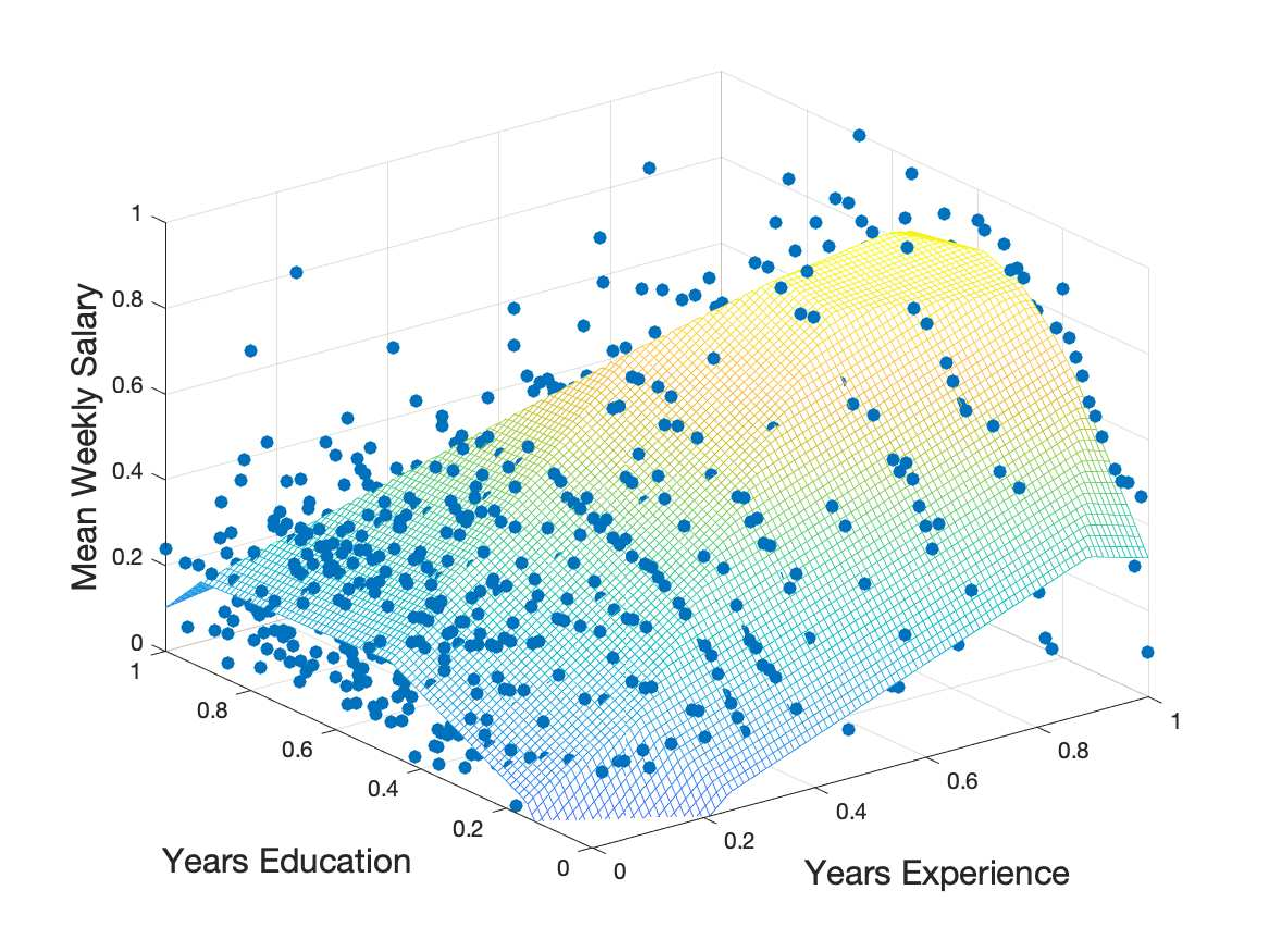
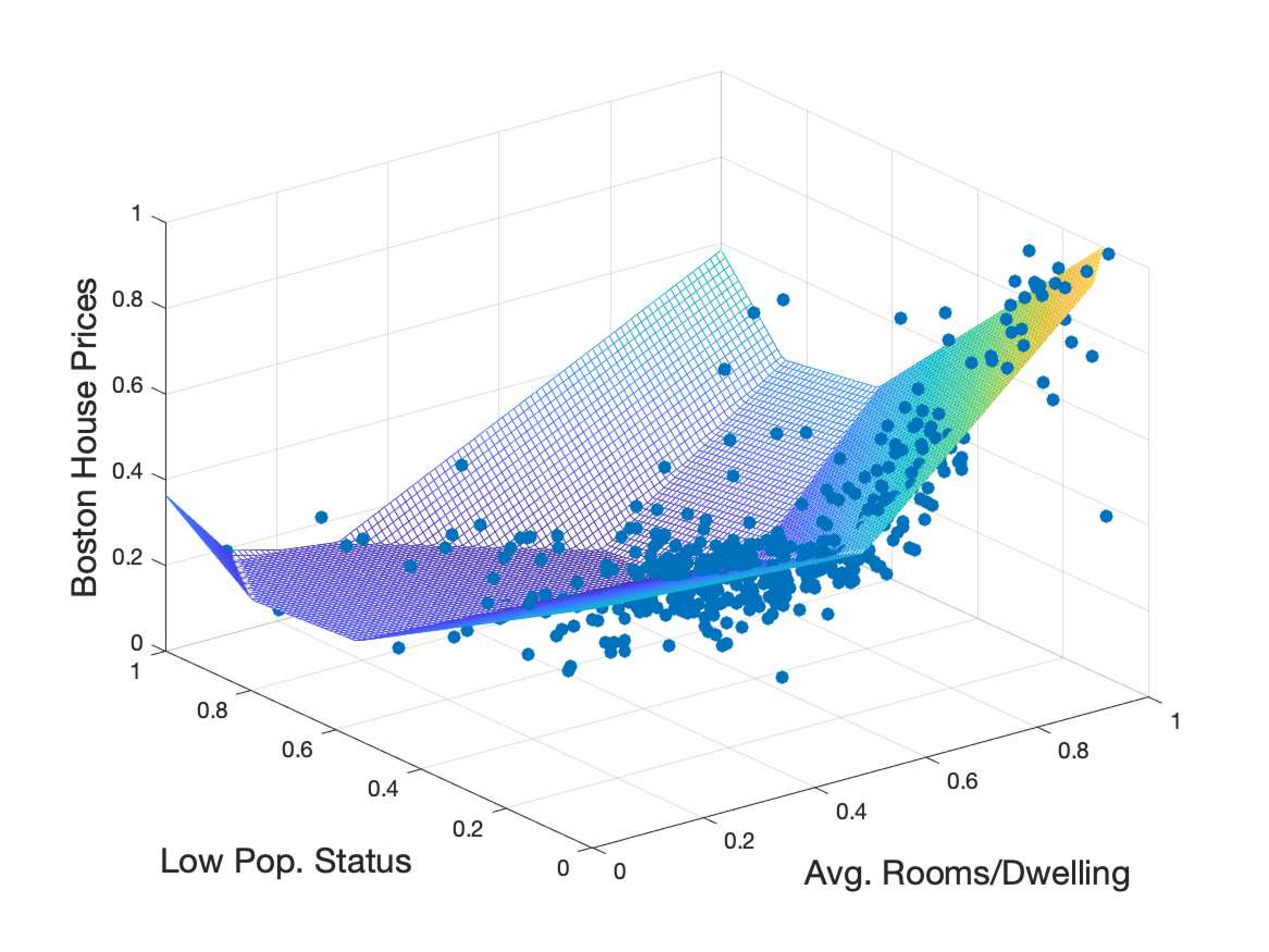
Max-Affine Regression

Max-affine regression recovers parameters in the max-affine function from its observations, which arise in statistics, economics, and machine learning. However, max-affine regression is challenging due to its non-convexity. We proposed two efficient algorithms.

First Order Methods: Gradient Descent (GD) and Stochastic Gradient Descent (SGD) are efficient and popular algorithms for solving non-convex optimization problems. We unveiled the effectiveness of first-order methods for max-affine regression through rigorous theoretical results. We demonstrate that first-order methods, when initialized near the ground-truth parameters, can solve the max-affine regression problem with linear convergence. The sample complexity is linear in terms of dimension, and polynomial in terms of certain geometrical parameters and the number of affine functions, with a high probability. Read More
Convex Program: We proposed a convex program to solve max-linear regression, which is a special case of max-affine regression. We show that this convex program can solve the max-affine regression problem with sample complexity comparable to the best-known results. Furthermore, we have demonstrated that our iterative version of the convex program is robust in outlier scenarios. Read More

Max-affine regression on mean weakly wages data — Max-affine model learned by SGD on mean weekly wages data

Max-affine regression on Boston house prices data — Max-affine model learned by SGD on Boston house prices data